exploring the undesigned
intelligence of the numberverse
lists/generators: Perfect Squares, Composites, Primes
"...out all day long.
All day long,
it goes on and on"
The First 1,000,000...
Generate Your Own Up to 1027...
Experimental Calculators
ZetaTest:
Infinite series
MinusSquare: Factoring
FermaticTest:
Probable prime
QTest:
Quadratic Series
RadiusTest:
Spiral lines and curves
PrimeTest
Analysis
Miller-Rabin:
Demonstration
Secrets of the Spiral
Proximate-Prime Polynomials
A proximate-prime polynomial is simply a quadratic equation - a finite polynomial of the second degree - that is derived from four successive (proximate, or neighboring) primes. Proximate-prime polynomials are interesting because they exhibit much greater prime densities than other polynomials.
The high primality of prime-derived quadratic sequences
What is a
"perfect prime polynomial"?
What is polynomial pronic
alignment?
Use an Excel spreadsheet to explore polynomial primes!
When you graph primes against an X-axis that treats the expanding interval between successive perfect squares as a constant unit subdivided into equal parts, you produce a distinctive wave form for primes and prime factors.
Try out an ingenious Excel worksheet to see the wave!
Counting primes by quadratic interval
How do you make Fermat's method of factorization faster than trial division...?
The Magic Square of Subtraction...
For every composite number that is not itself a perfect square there exists a pair of nonconsecutive perfect squares whose difference is equal to the composite. Even before we get to the subject of factorization, the consequences of this observation are fascinating and far-reaching.
Part
1 - A 'Classic Discovery'
Part 2 - A
Deterministic Test
It began with an exploration of biquadratic paired primes: 2 primes separated by the equivalent of exactly 2 quadratic intervals.... Then the investigation took the logical next level by asking the question: Are there prime pairs that are separated by other, greater multiples of the quadratic interval? And if there are, what are the frequency characteristics by interval size and perfect square offset? The results are in, with charts, an Excel visualization, and masses of half-digested data...!
Read about the latest
findings
What are Biquadratic Paired
Primes?
Two "new" rules of perfect squares
How I learned not to be
afraid of big numbers
It's a question of
magnitude...
Using Excel as a tool for number theory
Find examples throughout this site that demonstrate using VBA code with worksheets and graphing - including generating primes, perfect squares, and composites, doing modular arithmetic, calculating GCDs, and more....
|
Tools for Testing Natural Numbers |
|
| MinusSquare | |
| Miller-Rabin | |
| FermaticTest | |
| QTest | |
| RadiusTest | |
| ZetaTest | |
| PrimeTest | |
| |
|
| MinusSquare: Alternative Factoring Algorithm (beta) | |
|
The magic square of subtraction has given birth to a baby factoring algorithm. Download Program (25KB)
|
|
| |
|
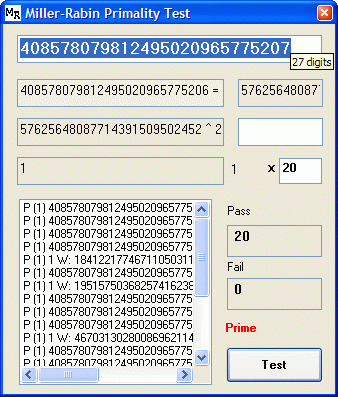
| Miller-Rabin Primality Test: Demo with source code (beta) | |
| |
Desktop program and complete project source code
for implementing the gold standard in primality
testing. A fast and reliable test for numbers up
to 1027-1 (that's 1 with 26 9s - a
prime number...!). Download Project (10KB) Download Program (17KB)
|
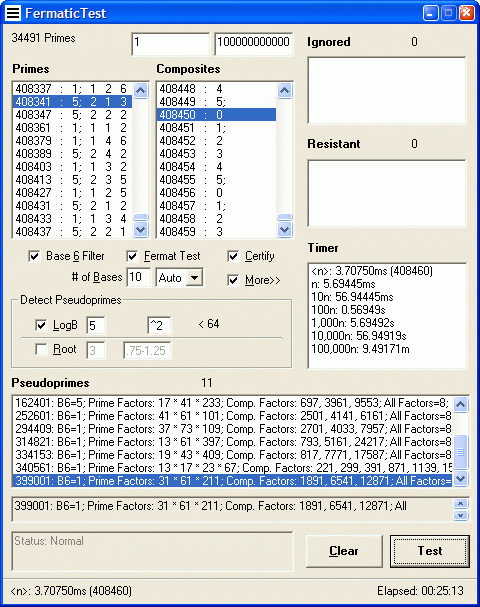
| FermaticTest: Prime and Pseudoprime Calculator | |
| |
"Fermatic" is a made-up word: Fermat + Automatic. This tool takes Fermat's great theorem to the limit, with some experiments to weed out pesky pseudoprimes. Rapidly generate prime, pseudoprime, and composite data. Download (34KB)
|
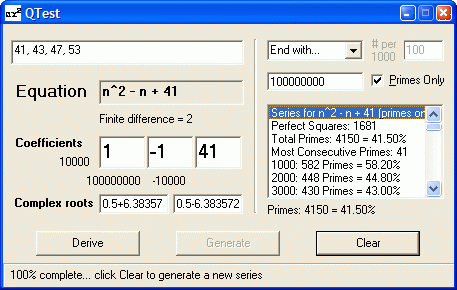
| QTest: Quadratic Sequence Calculator | |
| |
Enter 3 or 4 numbers in a sequence and find out what the next 10, next 1,000, or next 10,000 values are. QTest lets you derive a quadratic equation from the values you input (and solve the equation's roots). Then you can use this polynomial to generate and analyze long number sequences for primality. (See Robert Sacks' method for quadratic derivation, used in Vortex.) Download (35KB) How to Use QTest
|
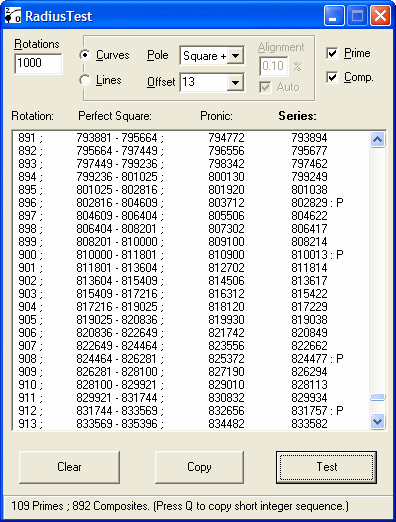
| RadiusTest: Polynomial Line and Curve Calculator | |
| |
Calculate prime and composite distribution in the Sacks Number Spiral by offset (curved series) and angle (straight series). Download (22KB)
|
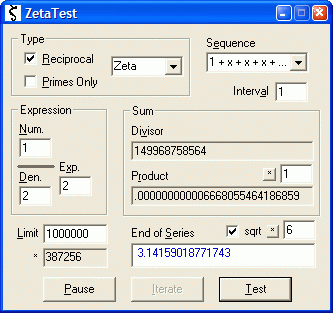
| ZetaTest: Infinite Series Calculator | |
| |
Calculate the products of infinite series using almost any inputs you can think of. Generates real number zeta series, demonstrating the calculation of many important constants - including e, pi, and phi, the Basel equality and Apéry's constant. Note: "Zeta" does not refer to the Riemann Zeta function for complex numbers.
Download (23KB)
|
| PrimeTest: Prime and Composite Analyzer | |
| |
Prime and composite number calculator (with prime and nonprime factor analyzer and prime number generator). Download (31KB) |
|
Tools that are digitally signed
are published by: Wordwise Solutions
|
|
|
|
|
Recommended sites: