exploring the undesigned
intelligence of the numberverse
Lists:Perfect Squares, Composites, Primes
First published November 8, 2009
| The problem with Fermat's factorization method is that it requires, on average, many more iterations than does simple trial division. However, it turns out that there's a simple fix for this. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
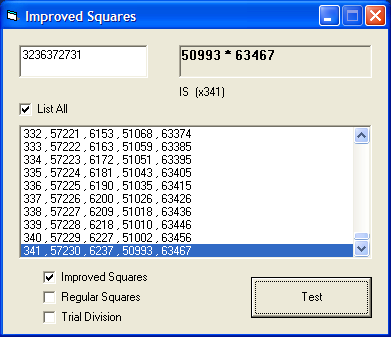
*OK, I acknowledge that trial div still has the edge for this baby example. Obviously, try something bigger for a fair test, say 9 or 10 digits. Remember that we're interested in the difficult ones - those with only 2 prime factors that are similar in size to the square root. A systematic survey by magnitude will be coming soon. Now you're ready to try this out for yourself. I've written some simple illustrative code comparing the "Improved Squares" method with the standard method and with trial division. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||