exploring the undesigned
intelligence of the numberverse
First published June 2, 2008
What is a semiprime?
A natural number that is the product of two prime numbers. *
*I originally observed Q factors to be proximate to the pair of perfect squares whose difference equals N. But, of course, if a GCD exists for N and a perfect square, it also exists for N and the root of that perfect square.
Therefore, it made sense to look systematically at all numbers (odd and even) less than N to see how often and how consistently the GCD equality holds.
Try it yourself: Generate semiprimes, their Q factors, and the charts shown on this page in Excel. Download the interactive worksheet.
| Graphing Q reveals an unexpected geometric thumbprint
- a
kind
of composite DNA - for every semiprime with distinct factors |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Definition of Q (as a subset of N*) For every composite N there exists a class of numbers less than N that share with N one of its factors as a GCD. In fact, we could call these numbers cofactors if that term was not already taken. (*This supersedes my original definition. ) It turns out that for what I term a symmetrical semiprime (one in which the two prime factors are distinct but are within an order of magnitude of each other), the number of Qs is about double the square root of N - sqrt(N)*2 - in other words, a lot...! (The reason for this is obvious if you read on.) When something occurs with a frequency twice that of a square root it becomes a very attractive candidate if your hunting factors. However, for now I'm going to consider just the geometric distribution of Q for what it is: a revelation in tessellation. So, in fact, a Q factor is any multiple of a prime factor less than N. The number of Qs for a given N must be equal to the sum of N's prime factors. Q factor tessellation occurs because, in the case of a semiprime, the cofactors of one prime factor intersect at even intervals with the cofactors of the other prime factor. The distribution of Q exhibits a multisymmetric geometric distribution when the Qs of any non-perfect-square semiprime are graphed. For semiprimes, the patterns are remarkable: an implicate order within every N that has common elements but is yet unique for each N. Semiprimes that are perfect squares - with a prime or nonprime factor - and composites with more than two prime factors do not demonstrate Q factor tessellation. The numbers do not look that interesting until you graph them.
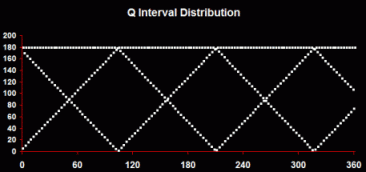
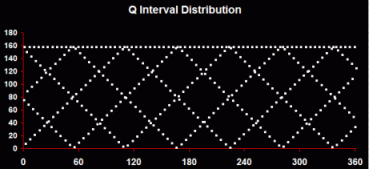
However, when you graph these numbers, they spring to life with brilliant precision. I've identified three distinctive types of patterns: Q Interval Distribution - By sorting the intervals between each Q according to the size of Q (in ascending or descending order).
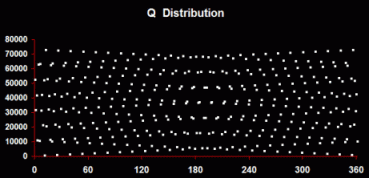
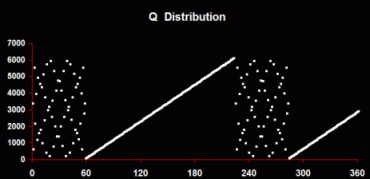
This produces the most characteristic and consistent pattern: a diamond lattice with one row or multiple rows. The vertices of the diamonds represent areas where Qs are concentrated (where the intervals are least). The horizontal top line represents the smaller of the semiprime's factors. Q Distribution - By sorting Q according to the size of the intervals between each Q (in ascending or descending order).
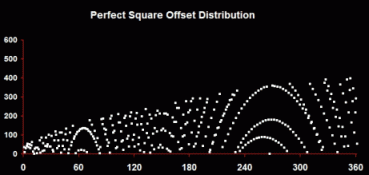
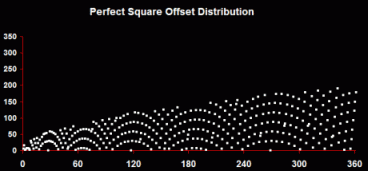
This produces the widest range of patterns, from complex organized distributions, to completely linear progressions, to graphs that combine both elements. Perfect Square Offset Distribution - The third kind of pattern - strictly, this is not tessellation - is created by looking at the differences between each Q and its immediately preceding perfect square.
These distributions produce the kind of intriguing patterns shown here - repeating curved symmetries with sprays and arches, partial or complete, as Q grows. Don't forget that these patterns are only apparent when multiple Q factors have been found - that is, the number must be factored first - and many times. Q factors provide the means of factoring and the means of understanding an undiscovered architecture of factors. Interim Conclusion
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||